Suite spectrale

En algèbre homologique et en topologie algébrique, une suite spectrale est un moyen de calculer des groupes de cohomologie par approximations successives. Ces suites ont été introduites par Jean Leray en 1946^[1], et sont depuis devenues un outil technique majeur en géométrie algébrique, complexe, ou en algèbre homologique. Par exemple, la suite spectrale de Serre (en) permet d'obtenir des informations sur les groupes d'homotopie des sphères.

Les séquences spectrales sont réputées difficiles à appréhender en raison de la grande quantité d'informations qu'elles mettent en jeu. Les cas les plus faciles à traiter sont ceux où la suite spectrale dégénère, ce qui signifie qu'une approximation supplémentaire ne produira aucune nouvelle information.

Historique et motivation

Motivé par des problèmes de topologie algébrique, Jean Leray a introduit la notion de faisceau et a chercher à calculer les groupes de cohomologie de faisceaux. C'est à cette occasion que Leray introduit la notion de suite spectrale. Étant donné un faisceau ${\displaystyle {\mathcal {F}}}$ sur un espace topologique ${\displaystyle X}$ et une application continue ${\displaystyle f:X\rightarrow Y}$, on peut pousser en avant ${\displaystyle {\mathcal {F}}}$, donnant un faisceau ${\displaystyle f^{*}{\mathcal {F}}}$ sur ${\displaystyle Y}$. Leray a constaté que les groupes de cohomologie du poussé en avant forment un complexe de chaînes naturel, de sorte que l'on peut prendre la cohomologie de la cohomologie. Il ne s'agit pas de la cohomologie du faisceau ${\displaystyle {\mathcal {F}}}$, mais celle-ci s'en rapproche en un certain sens. La cohomologie de la cohomologie forme à nouveau un complexe de chaînes, on opère le même procédé et ainsi de suite. À la limite de ce processus, le résultat est essentiellement la cohomologie du faisceau initial.

On s'est rendu compte que la technique de calcul de Leray était un exemple d'un phénomène plus général. Bien que leur importance théorique ait reculé depuis l'introduction des catégories dérivées, elles restent l'outil de calcul cohomologique le plus systématique et efficace qui soit.

Définition

Suite spectrale homologique

Soit une catégorie abélienne (e.g. les modules  sur un anneau), et un entier non négatif ${\displaystyle r_{0}}$. Une suite spectrale homologique est une collection ${\displaystyle \{E_{r},d_{r}\}_{r\geq r_{0}}}$ d'objets ${\displaystyle E_{r}}$ et d'endomorphismes ${\displaystyle d_{r}:E_{r}\to E_{r}}$, tel que pour tout ${\displaystyle r\geq r_{0}}$

1. ${\displaystyle d_{r}\circ d_{r}=0}$,
2. ${\displaystyle E_{r+1}\cong H_{*}(E_{r},d_{r})}$, l'homologie de ${\displaystyle E_{r}}$ par rapport à ${\displaystyle d_{r}}$.

Par habitude, les isomorphismes sont supprimés et on écrit ${\displaystyle E_{r+1}=H_{*}(E_{r},d_{r})}$. Un objet ${\displaystyle E_{r}}$ est appelé une « page », ou encore un « terme » ; les endomorphismes ${\displaystyle d_{r}}$ les « différentielles ». Et, ${\displaystyle E_{r+1}}$ est appelé « l'objet dérivé » de ${\displaystyle E_{r}}$.

Suite spectrale bigraduée

En réalité, les suites spectrales se produisent principalement dans la catégorie des modules  bigradués sur un anneau R, c'est-à-dire que chaque page est un R-module bigradué ${\textstyle E_{r}=\bigoplus _{p,q\in \mathbb {Z} ^{2}}E_{r}^{p,q}}$. Une suite spectrale cohomologique est alors une suite ${\displaystyle \{E_{r},d_{r}\}_{r\geq r_{0}}}$ de R-modules bigradués ${\displaystyle \{E_{r}^{p,q}\}_{p,q}}$, et pour chaque module une famille d'endomorphismes ${\displaystyle d_{r}=(d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1})_{p,q\in \mathbb {Z} ^{2}}}$ de bidegré ${\displaystyle (r,1-r)}$. On demande pour ${\displaystyle r\geq r_{0}}$ :

1. ${\displaystyle d_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}=0}$,
2. ${\displaystyle E_{r+1}\cong H^{*}(E_{r},d_{r})}$.

Selon la suite spectrale, la première age peut avoir un degré égal à r = 0, 1 ou 2. Par exemple, pour le suite spectrale d'un complexe filtré décrite ci-dessous, on a r₀ = 0, mais pour la suite spectrale de Grothendieck, on a r₀ = 2.

Suite spectrale d'un complexe de chaînes

On se place dans l'hypothèse non gradué. La suite spectrale associée à un complexe de chaînes C_• donne l'exemple le plus simple dans ce cas. Soit d la différentielle associée au complexe. Soit r₀ = 0, et E₀ étant définit par C_•. Par conséquent, E₁ est le complexe H(C_•) : Le i-ème terme du complexe E₁ calcul le i-ème groupe de (co)homologie de C_•. La seule différentielle naturelle sur ce nouveau complexe est la différentielle nulle : d₁ = 0. Cela force ${\displaystyle E_{2}}$ à être égal à ${\displaystyle E_{1}}$. La suite spectrale dégénère en page 1. Pour résumer :

• E₀ est le complexe C_•,
• E₁ est le complexe H(C_•) pour r ≥ 1.

L'information de la suite spectrale est concentrée en degré 0 et 1 : aller calculer les pages supérieures ne sert pas. Il faut habituellement une structure supplémentaire sur les E_r, pour obtenir des informations utiles en pages supérieures.

Illustration

Une suite spectrale bigraduée contient une grande quantité d'information à suivre. Il existe des illustrations qui rendent la structure de la suite spectrale plus claire. Nous avons trois indices, r, p et q. Un objet ${\displaystyle E_{r}}$ peut être vu comme la ${\displaystyle r}$-ième page d'un livre à carreaux. Sur ces pages, p désigne la direction horizontale et q la verticale. À chaque point du réseau, nous avons l'objet ${\displaystyle E_{r}^{p,q}}$. Passer à la page suivante signifie prendre l'homologie (resp. la cohomologie), c'est-à-dire que la ${\displaystyle r+1}$-ième page est un sous-quotient de la ${\displaystyle r}$-ième page. Dans le cas homologique, les différentielles ont un bidegré (−r, r − 1), donc n diminue de un d'une page à l'autre. Dans le cas cohomologique, n est augmenté de un.

Propriétés

Propriétés catégorielles

L'ensemble des suite spectrales cohomologiques forment une catégorie. Une flèche dans cette catégorie ${\displaystyle f:E\to E'}$ est par définition une collection de morphismes ${\displaystyle f_{r}:E_{r}\to E'_{r}}$ compatibles avec la différentielles, i.e. ${\displaystyle f_{r}\circ d_{r}=d'_{r}\circ f_{r}}$, et avec l'isomorphisme entre la cohomologie de la r-ième page et la (r+1)-ième page de E et E', c'est-à-dire: ${\displaystyle f_{r+1}(E_{r+1})\,=\,f_{r+1}(H(E_{r}))\,=\,H(f_{r}(E_{r}))}$. Dans le cas bigradué, les morphismes doivent de plus conserver la graduation: ${\displaystyle f_{r}(E_{r}^{p,q})\subset {E'_{r}}^{p,q}.}$

Structure multiplicative

Un cup-produit donne une structure d'anneau à un groupe de cohomologie, le transformant en un anneau de cohomologie. Ainsi, il est naturel de considérer une structure d'anneaux sur la suite spectrale. Soit ${\displaystyle E_{r}^{p,q}}$ une suite spectrale de type cohomologique. On dit qu'elle a une structure multiplicative si

1. ${\displaystyle E_{r}}$ est une algèbre différentielle graduée (ou bigraduée) ;
2. La multiplication sur ${\displaystyle E_{r+1}}$ est induite par celle sur ${\displaystyle E_{r}}$.

Un exemple est donné par la suite spectrale de Serre cohomologique associée à une fibration ${\displaystyle F\to E\to B}$, lorsque le groupe de coefficients est un anneau R^[2],[3]. La structure multiplicative peut être très utile pour calculer des différentielles de la suite^[4].

Constructions de suites spectrales

Les suite spectrales peuvent être construites de différentes manières. En topologie algébrique, un couple exact est peut-être l’outil de construction le plus courant. En géométrie algébrique, les suites spectrales sont généralement construites à partir de filtrations de complexes de cochaînes.

Suite spectrale d'un couple exact

Une première construction de suites spectrales est la méthode des couples exacts de William Massey, devenus courants en topologie algébrique ; mais bien moins en algèbre.

Pour définir des couples exacts, on se donne une catégorie abélienne. Comme ce-dessus, dans la pratique, il s'agit généralement de modules bigradués sur un anneau. Un couple exact est une paire d'objets (A, C), munie de trois homomorphismes entre ces objets : f : A → A, g : A → C et h : C → A vérifiants les conditions d'exactitudes :

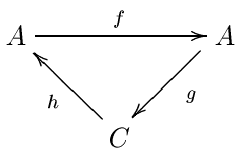
• Im f = Ker g
• Im g = Ker h
• Im h = Ker f

On notera cette donnée (A, C, f, g, h), représentée par un triangle. le terme C correspond à la première page E₀ de la suite spectrale et A est une donnée auxiliaire.

Pour passer à la page suivante, on définit le couple dérivé. Soit :

• d = g o h
• A' = f(A)
• C' = Ker d / Im d
• f' = f|_A', la restriction de f à A'
• h' : C' → A' induit par h.
• g' : A' → C' et définie comme suit: Pour tout a dans A', on note a = f(b) pour un certain b dans A. g'(a) est définit comme étant l'image de g(b) dans C'.

Il est immédiat de vérifier que le couple (A', C', f', g', h') est exact. C' correspond au terme E₁ de la suite spectrale. On définit par récurrence la suite (A⁽ⁿ⁾, C⁽ⁿ⁾, f⁽ⁿ⁾, g⁽ⁿ⁾, h⁽ⁿ⁾).

Les différentielles de la suite spectrale sont données par,d_n = g⁽ⁿ⁾ o h⁽ⁿ⁾ et E_n = C⁽ⁿ⁾.

Exemples de suites spectrales

• Suite spectrale de Serre (en)^[5] - calculant la (co)homologie d'une fibration.
• Suite spectrale d'Atiyah-Hirzebruch (en) - calculant la (co)homologie en K-théorie.
• Suite spectrale de Bockstein (en)

Suite spectrale d'un complexe filtré

Une méthode courante de construction de suite spectrale provient d'un complexe de cochaînes filtré, car celui-ci induit naturellement un objet biggradué. Soit un complexe de cochaînes ${\displaystyle (C^{\bullet },d)}$ avec une filtration descendante, ${\textstyle ...\supset \,F^{-2}C^{\bullet }\,\supset \,F^{-1}C^{\bullet }\supset F^{0}C^{\bullet }\,\supset \,F^{1}C^{\bullet }\,\supset \,F^{2}C^{\bullet }\,\supset \,F^{3}C^{\bullet }\,\supset ...\,}$. On impose que les différentielles du complexe soit compatible avec la filtration, i.e. ${\textstyle d(F^{p}C^{n})\subset F^{p}C^{n+1}}$, et que la filtration soit exhaustive, c'est-à-dire que l'union de l'ensemble des ${\textstyle F^{p}C^{\bullet }}$ est égal au complexe entier ${\textstyle C^{\bullet }}$. Il existe une suite spectrale en posant${\textstyle E_{0}^{p,q}=F^{p}C^{p+q}/F^{p+1}C^{p+q}}$ et ${\textstyle E_{1}^{p,q}=H^{p+q}(F^{p}C^{\bullet }/F^{p+1}C^{\bullet })}$^[6]. On supposera aussi que la filtration est séparée, c'est-à-dire que l'intersection des ensembles ${\textstyle F^{p}C^{\bullet }}$ est nulle.

La filtration est utile car elle donne une mesure de proximité de zéro : à mesure que p augmente, ${\textstyle F^{p}C^{\bullet }}$ se « rapproche » de plus en plus de zéro.

Construction de la suite

${\displaystyle C^{\bullet }}$ n'est munie que d'une seule filtration, nous construisons donc d'abord un objet doublement gradué pour la première page de la suite spectrale. On note :

${\displaystyle Z_{-1}^{p,q}=Z_{0}^{p,q}=F^{p}C^{p+q}}$

${\displaystyle B_{0}^{p,q}=0}$

${\displaystyle E_{0}^{p,q}={\frac {Z_{0}^{p,q}}{B_{0}^{p,q}+Z_{-1}^{p+1,q-1}}}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}}}$

${\displaystyle E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q}}$

Puisque nous avons supposé que les applications sont compatibles à la filtration, ${\displaystyle E_{0}}$ est un objet bigradué et on a une différentielle ${\displaystyle d_{0}}$ sur ${\displaystyle E_{0}}$. Pour obtenir ${\displaystyle E_{1}}$, on prend l'homologie de ${\displaystyle E_{0}}$.

${\displaystyle {\bar {Z}}_{1}^{p,q}=\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}=\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}}$

${\displaystyle {\bar {B}}_{1}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}}$

${\displaystyle E_{1}^{p,q}={\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}}$

${\displaystyle E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}=\bigoplus _{p,q\in \mathbf {Z} }{\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}}$

Noter que ${\displaystyle {\bar {Z}}_{1}^{p,q}}$ et ${\displaystyle {\bar {B}}_{1}^{p,q}}$ peuvent être écrits comme images dans ${\displaystyle E_{0}^{p,q}}$ de

${\displaystyle Z_{1}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+1}C^{p+q+1}}$

${\displaystyle B_{1}^{p,q}=({\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

de sorte que l'on puisse écrire

${\displaystyle E_{1}^{p,q}={\frac {Z_{1}^{p,q}}{B_{1}^{p,q}+Z_{0}^{p+1,q-1}}}.}$

${\displaystyle Z_{1}^{p,q}}$ sont les éléments dont le degré dans la filtration augmentent de un par la différentielle, et ${\displaystyle B_{1}^{p,q}}$ sont les images des éléments dont le degré dans la filtration n'augmente pas par la différentielle. Cela suggère la definition de ${\displaystyle Z_{r}^{p,q}}$ et ${\displaystyle B_{r}^{p,q}}$ :

${\displaystyle Z_{r}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1}}$

${\displaystyle B_{r}^{p,q}=({\mbox{im }}d_{0}^{p-r+1,q+r-2}:F^{p-r+1}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

${\displaystyle E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{B_{r}^{p,q}+Z_{r-1}^{p+1,q-1}}}}$

avec la relation

${\displaystyle B_{r}^{p,q}=d_{0}^{p,q}(Z_{r-1}^{p-r+1,q+r-2}).}$

Pour que ${\displaystyle d_{r}}$ soit bien définie sur chaque ${\displaystyle E_{r}}$ et donnant l'homologie en passant à ${\displaystyle E_{r+1}}$, l'application

${\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}}$

est définie par restriction de ${\displaystyle d}$ définie sur ${\displaystyle C^{p+q}}$ au sous-objet ${\displaystyle Z_{r}^{p,q}}$. On vérifie aisément que l'homologie selon cette différentielle de ${\displaystyle E_{r}}$ est ${\displaystyle E_{r+1}}$, donnant ainsi une suite spectrale. Seulement, la définition de ${\displaystyle d_{r}}$ n'est pas explicite.

Exemples de suites spectrales

• Suite spectrale de Hodge-de Rham (en)
• Peut être utilisée pour la construction des modules de Hodge mixtes^[7].

Convergence, dégénérescence

Soit E_r une suite spectrale, partant de r = 1. Il existe donc une suite de sous-objets :

${\displaystyle 0=B_{0}\subset B_{1}\subset B_{2}\subset \dots \subset B_{r}\subset \dots \subset Z_{r}\subset \dots \subset Z_{2}\subset Z_{1}\subset Z_{0}=E_{1}}$

tels que ${\displaystyle E_{r}\simeq Z_{r-1}/B_{r-1}}$; on pose en effet ${\displaystyle Z_{0}=E_{1},B_{0}=0}$ et ${\displaystyle Z_{r},B_{r}}$ tels que ${\displaystyle Z_{r}/B_{r-1},B_{r}/B_{r-1}}$ sont le noyau et l'image de ${\displaystyle E_{r}{\overset {d_{r}}{\to }}E_{r}.}$ On pose alors ${\displaystyle Z_{\infty }=\cap _{r}Z_{r},B_{\infty }=\cup _{r}B_{r}}$ et${\displaystyle E_{\infty }=Z_{\infty }/B_{\infty }}$, le terme limite. (Un tel ${\displaystyle E_{\infty }}$ n'existe pas forcément dans la catégorie, mais existe presque toujours en pratique ; due à la finitude de l'union.)

Termes de convergence

On dit qu'une suite converge faiblement s'il existe un objet gradué ${\displaystyle H^{\bullet }}$ avec une filtration ${\displaystyle F^{\bullet }H^{n}}$ pour tout ${\displaystyle n}$, et pour tout ${\displaystyle p}$ il existe un isomorphisme ${\displaystyle E_{\infty }^{p,q}\cong F^{p}H^{p+q}/F^{p+1}H^{p+q}}$. La suite converge à ${\displaystyle H^{\bullet }}$ si la filtration ${\displaystyle F^{\bullet }H^{n}}$ est séparée (i.e. ${\displaystyle \cap _{p}F^{p}C^{\bullet }=0}$). On note

${\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{n}}$

pour signifier que pour p + q = n, ${\displaystyle E_{r}^{p,q}}$ converge vers ${\displaystyle E_{\infty }^{p,q}}$. On dit qu'une suite spectrale ${\displaystyle E_{r}^{p,q}}$ aboutit à ${\displaystyle E_{\infty }^{p,q}}$ si pour tout ${\displaystyle p,q}$ on a un entier ${\displaystyle r(p,q)}$ tel que pour tout ${\displaystyle r\geq r(p,q)}$, ${\displaystyle E_{r}^{p,q}=E_{r(p,q)}^{p,q}}$. Alors ${\displaystyle E_{r(p,q)}^{p,q}=E_{\infty }^{p,q}}$ est le terme limite. La suite spectral dégénèrer à ${\displaystyle r_{0}}$ si les différentielles ${\displaystyle d_{r}^{p,q}}$ sont nulles pour tout ${\displaystyle r\geq r_{0}}$. On le note:

${\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}}$

Il est usuel d'écrire à droite ${\displaystyle E_{2}^{p,q}}$, la plupart des suites spectrales aboutissants en deuxième page.

Exemples de dégénérescence

Suite spectrale d'un complexe filtré, suite

On repart de la construction à partir du complexe de cochaînes ${\displaystyle (C^{\bullet },d)}$ avec filtration descendante. On remarque la suite d'inclusion

${\displaystyle Z_{0}^{p,q}\supseteq Z_{1}^{p,q}\supseteq Z_{2}^{p,q}\supseteq \cdots \supseteq B_{2}^{p,q}\supseteq B_{1}^{p,q}\supseteq B_{0}^{p,q}}$

On peut alors se demander si, en définissant

${\displaystyle Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q},}$

${\displaystyle B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q},}$

${\displaystyle E_{\infty }^{p,q}={\frac {Z_{\infty }^{p,q}}{B_{\infty }^{p,q}+Z_{\infty }^{p+1,q-1}}}.}$

${\displaystyle E_{\infty }^{p,q}}$ serait un candidat naturel pour le terme limite. Pour décrire plus en détail l'aboutissement de la suite spectrale, notons que nous avons les formules :

${\displaystyle Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q}=\bigcap _{r=0}^{\infty }\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1})}$

${\displaystyle B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q}=\bigcup _{r=0}^{\infty }({\mbox{im }}d^{p,q-r}:F^{p-r}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

Puisque la suite est séparée, les noyaux décroisent en r jusqu'à${\displaystyle Z_{\infty }^{p,q}=\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1})}$. Pour ${\displaystyle B_{\infty }^{p,q}}$, rappelons que la suite a été supposée exhaustive. Les images croissent jusqu'à${\displaystyle B_{\infty }^{p,q}={\text{im }}(C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$. On en déduit finalement que

${\displaystyle E_{\infty }^{p,q}={\mbox{gr}}_{p}H^{p+q}(C^{\bullet })}$,

c'est-à-dire que la suite spectrale abouti vers la p-ième partie graduée du (p+q)-ième groupe d'homologie de C. Si la suite spectrale converge, on en déduit que :

${\displaystyle E_{r}^{p,q}\Rightarrow _{p}H^{p+q}(C^{\bullet })}$

Suites exactes longues

En utilisant la séquence spectrale d’un complexe filtré, nous pouvons déduire l’existence de suites exactes longues. Soit une suite exacte courte de complexes de cochaînes 0 → A^• → B^• → C^• → 0, et f^• : A^• → B^•. On obtient naturellement la suite de cohomologie Hⁿ(A^•) → Hⁿ(B^•) → Hⁿ(C^•) exacte au centre. On filtre le complexe B^• comme suit :

${\displaystyle F^{0}B^{n}=B^{n}}$

${\displaystyle F^{1}B^{n}=A^{n}}$

${\displaystyle F^{2}B^{n}=0}$

Donnant

${\displaystyle E_{0}^{p,q}={\frac {F^{p}B^{p+q}}{F^{p+1}B^{p+q}}}={\begin{cases}0&{\text{si }}p<0{\text{ ou }}p>1\\C^{q}&{\text{si }}p=0\\A^{q+1}&{\text{si }}p=1\end{cases}}}$

${\displaystyle E_{1}^{p,q}={\begin{cases}0&{\text{si }}p<0{\text{ ou }}p>1\\H^{q}(C^{\bullet })&{\text{si }}p=0\\H^{q+1}(A^{\bullet })&{\text{si }}p=1\end{cases}}}$

La différentielle est de bidegrée (1, 0), donc d_0,q : H^q(C^•) → H^q+1(A^•). Le lemme du serpent A^• → B^• → C^• donne une suite de complexes :

${\displaystyle \cdots \rightarrow H^{q}(B^{\bullet })\rightarrow H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\rightarrow \cdots }$

Il reste à montrer que cette suite est exacte en les groupes associés à A et C. Notons que la suite dégénère en E₂ (par degré de la différentielle). Par conséquent, le terme E₂ est égal à E_∞ :

${\displaystyle E_{2}^{p,q}\cong {\text{gr}}_{p}H^{p+q}(B^{\bullet })={\begin{cases}0&{\text{si }}p<0{\text{ ou }}p>1\\H^{q}(B^{\bullet })/H^{q}(A^{\bullet })&{\text{si }}p=0\\{\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })&{\text{si }}p=1\end{cases}}}$

Mais nous avons aussi une description directe du terme E₂ comme homologie du terme E₁. Ces deux descriptions doivent être isomorphes :

${\displaystyle H^{q}(B^{\bullet })/H^{q}(A^{\bullet })\cong \ker d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })}$

${\displaystyle {\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\cong H^{q+1}(A^{\bullet })/({\mbox{im }}d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet }))}$

Le premier donne l'exactitude en C, et le second en les groupes de cohomologie en A.

Suite spectrale d'un complexe bigradué

On trouve pour un complexe bigradué que :

${\displaystyle H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))\Rightarrow _{p}H^{p+q}(T(C_{\bullet ,\bullet }))}$

${\displaystyle H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet }))\Rightarrow _{q}H^{p+q}(T(C_{\bullet ,\bullet }))}$

Remarquer qu'en général, les deux filtrations sur H^p+q(T(C_•,•)) sont distinctes.

Exemples

Pages en premier quadrant

Soit une suite spectrale où ${\displaystyle E_{r}^{p,q}}$ s'annule pour tout ${\displaystyle p}$ et ${\displaystyle q}$ négatif, dit suite spectrale en premier quadrant. La suite aboutie car on a ${\displaystyle E_{r+i}^{p,q}=E_{r}^{p,q}}$ pour tout ${\displaystyle i\geq 0}$ si ${\displaystyle r>p}$ et ${\displaystyle r>q+1}$.

Deux colonnes adjacentes

Soit ${\displaystyle E_{p,q}^{r}}$ une suite spectrale homologique telles que ${\displaystyle E_{p,q}^{2}=0}$ pour tout p autre que 0, 1. Visuellement, la deuxième page ${\displaystyle E^{2}}$ est :

${\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&E_{1,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&E_{1,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&E_{1,0}^{2}&0&\cdots \\\cdots &0&E_{0,-1}^{2}&E_{1,-1}^{2}&0&\cdots \\&\vdots &\vdots &\vdots &\vdots &\end{matrix}}}$

Les différentielles en seconde page ont bidegrée (-2, 1), donc s'écrivent

${\displaystyle d_{p,q}^{2}:E_{p,q}^{2}\to E_{p-2,q+1}^{2}}$

Ces applications sont toutes nulles car

${\displaystyle d_{0,q}^{2}:E_{0,q}^{2}\to 0}$, ${\displaystyle d_{1,q}^{2}:E_{1,q}^{2}\to 0}$

ainsi la suite spectrale dégénère : ${\displaystyle E^{\infty }=E^{2}}$. Elle converge vers, disons, ${\displaystyle H_{*}}$ avec une filtration

${\displaystyle 0=F_{-1}H_{n}\subset F_{0}H_{n}\subset \dots \subset F_{n}H_{n}=H_{n}}$

telle que ${\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}/F_{p-1}H_{p+q}}$. Alors ${\displaystyle F_{0}H_{n}=E_{0,n}^{2}}$, ${\displaystyle F_{1}H_{n}/F_{0}H_{n}=E_{1,n-1}^{2}}$, ${\displaystyle F_{2}H_{n}/F_{1}H_{n}=0}$, ${\displaystyle F_{3}H_{n}/F_{2}H_{n}=0}$, etc. On a donc une suite exacte courte^[8] :

${\displaystyle 0\to E_{0,n}^{2}\to H_{n}\to E_{1,n-1}^{2}\to 0}$.

Deux lignes adjacentes

De même, on considère ${\displaystyle E_{p,q}^{r}}$ une suite spectrale concentrée en page deux sur les lignes q = 0, 1. Contrairement au cas précédent, elle ne dégénère pas nécessairement en page deux, mais sûrement en page trois.

Supposons que la suite converge vers H avec une filtration F comme dans l'exemple précédent. Puisque ${\displaystyle F_{p-2}H_{p}/F_{p-3}H_{p}=E_{p-2,2}^{\infty }=0}$, ${\displaystyle F_{p-3}H_{p}/F_{p-4}H_{p}=0}$, etc., on a: ${\displaystyle 0\to E_{p-1,1}^{\infty }\to H_{p}\to E_{p,0}^{\infty }\to 0}$, et finalement^[9] :

${\displaystyle \cdots \to H_{p+1}\to E_{p+1,0}^{2}{\overset {d}{\to }}E_{p-1,1}^{2}\to H_{p}\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to H_{p-1}\to \dots .}$

Suite de Wang

Le calcul de la section précédente se généralise de manière simple. Considérons une fibration sur une sphère :

${\displaystyle F{\overset {i}{\to }}E{\overset {p}{\to }}S^{n}}$

avec n supérieur ou égal à 2. Nous avons la suite spectrale de Serre :

${\displaystyle E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))\Rightarrow H_{p+q}(E)}$;

C'est-à-dire que ${\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}(E)/F_{p-1}H_{p+q}(E)}$ avec une filtration ${\displaystyle F_{\bullet }}$.

On sait que ${\displaystyle H_{p}(S^{n})}$ est non nulle si p ou n vaut zéro et vaut Z dans ce cas, on voit que ${\displaystyle E_{p,q}^{2}}$ consiste en seulement deux lignes ${\displaystyle p=0,n}$, Ainsi la page en ${\displaystyle E^{2}}$ est donnée par

${\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&0&\cdots &0&E_{n,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&0&\cdots &0&E_{n,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&0&\cdots &0&E_{n,0}^{2}&0&\cdots \\\end{matrix}}}$

De plus, sachant

${\displaystyle E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))=H_{q}(F)}$

pour ${\displaystyle p=0,n}$ par le théorème des coefficients universels, ${\displaystyle E^{2}}$ s'illustre comme suit :

${\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&H_{2}(F)&0&\cdots &0&H_{2}(F)&0&\cdots \\\cdots &0&H_{1}(F)&0&\cdots &0&H_{1}(F)&0&\cdots \\\cdots &0&H_{0}(F)&0&\cdots &0&H_{0}(F)&0&\cdots \\\end{matrix}}}$

La seule différentielle non nulle en page ${\displaystyle E^{n}}$ est donnée par

${\displaystyle d_{n,q}^{n}:E_{n,q}^{n}\to E_{0,q+n-1}^{n}}$

qui est

${\displaystyle d_{n,q}^{n}:H_{q}(F)\to H_{q+n-1}(F)}$

La suite spectrale converge en page ${\displaystyle E^{n+1}=E^{\infty }}$. On en déduit une suite exacte

${\displaystyle 0\to E_{n,q-n}^{\infty }\to E_{n,q-n}^{n}{\overset {d}{\to }}E_{0,q-1}^{n}\to E_{0,q-1}^{\infty }\to 0.}$

c'est-à-dire :

${\displaystyle 0\to E_{n,q-n}^{\infty }\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F)\to E_{0,q-1}^{\infty }\to 0.}$

Pour expliciter les termes en ${\displaystyle E^{\infty }}$, notons ${\displaystyle H=H(E)}$. Puisque${\displaystyle F_{1}H_{q}/F_{0}H_{q}=E_{1,q-1}^{\infty }=0}$, etc., on a: ${\displaystyle E_{n,q-n}^{\infty }=F_{n}H_{q}/F_{0}H_{q}}$ et donc, avec ${\displaystyle F_{n}H_{q}=H_{q}}$,

${\displaystyle 0\to E_{0,q}^{\infty }\to H_{q}\to E_{n,q-n}^{\infty }\to 0.}$

D'où une suite exacte

${\displaystyle 0\to H_{q}(F)\to H_{q}(E)\to H_{q-n}(F)\to 0.}$

Ainsi, on en déduit avec tout cela la suite exacte longue^[10] :

${\displaystyle \dots \to H_{q}(F){\overset {i_{*}}{\to }}H_{q}(E)\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F){\overset {i_{*}}{\to }}H_{q-1}(E)\to H_{q-n-1}(F)\to \dots }$

(La suite de Gysin est obtenue de manière similaire.)

Suites notoires

Quelques suites spectrales notoires :

Topologie et géométrie

Homologie

Algèbre

Géométrie complexe et algébrique

Articles connexes

• Cohomologie
• Transgression

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Spectral sequence » (voir la liste des auteurs).

Notes

Références

• Jean Leray, L'anneau d'homologie d'une représentation, vol. 222, 1946a, 1366–1368 p.
• Jean Leray, Structure de l'anneau d'homologie d'une représentation, vol. 222, 1946b, 1419–1422 p.
• Jean-Louis Koszul, « Sur les opérateurs de dérivation dans un anneau », Comptes rendus de l'Académie des sciences, vol. 225,‎ 1947, p. 217–219
• Séminaire Henri Cartan de l'École Normale Supérieure, 1950/1951. Cohomologie des groupes, suite spectrale, faisceaux
• (en) Allen Hatcher, Spectral Sequences in Algebraic Topology, 2004 (lire en ligne)
• (en) John McCleary, A User's Guide to Spectral Sequences, Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics », 2000, 578 p. (ISBN 978-0-521-56759-6, lire en ligne)
• (en) Robert Mosher et Martin Tangora, Cohomology Operations and Applications in Homotopy Theory
• (en)Anatoly Fomenko et Dmitry Fuchs, Homotopical Topology (lire en ligne)
• (en) William S. Massey, « Exact couples in algebraic topology. I, II », Annals of Mathematics, vol. 56, n^o 2,‎ 1952, p. 363–396 (DOI 10.2307/1969805, JSTOR 1969805)
• (en) William S. Massey, « Exact couples in algebraic topology. III, IV, V », Annals of Mathematics, vol. 57, n^o 2,‎ 1953, p. 248–286 (DOI 10.2307/1969858, JSTOR 1969858)
• (en) J. Peter May, « A primer on spectral sequences » [archive du 21 juin 2020] (consulté le 21 juin 2020)
• (en) John McCleary, A User's Guide to Spectral Sequences, vol. 58, Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics », 2001, 2nd éd. (ISBN 978-0-521-56759-6, MR 1793722)
• (en) Robert Mosher et Martin Tangora, Cohomology Operations and Applications in Homotopy Theory, Harper and Row, 1968 (ISBN 978-0-06-044627-7)
• Charles A. Weibel, An introduction to homological algebra, vol. 38, Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics », 1994 (ISBN 978-0-521-55987-4, OCLC 36131259, MR 1269324)

• Portail des mathématiques