Log-polära koordinater

Log-polära koordinater (förkortning för logaritmiskt polära koordinater) är en form av koordinatsystem i två dimensioner där en punkt identifieras av två tal, ett för logaritmen på avståndet från en fix punkt, och ett för en vinkel. Log-polära koordinater är nära besläktade med polära koordinater, som traditionellt används för att beskriva områden i planet med någon form av rotationssymmetri. Inom områden som harmonisk och komplex analys är log-polära koordinater mer naturliga än polära.

Definition och koordinattransformationer

Log-polära koordinater i planet består av ett par (ρ,θ) av reella tal, där ρ är logaritmen på avståndet till en given punkt (origo) och θ är vinkeln mellan en referenslinje (x-axeln) och linjen som går genom origo och punkten. Vinkelkoordinaten är densamma som för polära koordinater, medan sambandet för den radiella koordinaten är givet av

${\displaystyle r=e^{\rho }}$.

där r är avståndet till origo. Formlerna för transformering från kartesiska koordinater till log-polära koordinater är

${\displaystyle {\begin{cases}\rho =\log {\sqrt {x^{2}+y^{2}}}\\\theta =\arctan {y/x}\end{cases}}}$.

och formlerna för transformering från log-polära koordinater till kartesiska är

${\displaystyle {\begin{cases}x=e^{\rho }\cos \theta \\y=e^{\rho }\sin \theta .\end{cases}}}$

Genom att använda komplexa tal (x,y) = x+iy ser vi att den sistnämnda koordinattransformationen är given av den komplexa exponentialfunktionen

${\displaystyle x+iy=e^{\rho +i\theta }}$.

Detta får som konsekvens att grundläggande ekvationer inom harmonisk analys och komplex analys får samma enkla form i log-polära koordinater som i kartesiska. Detta är inte fallet med polära koordinater.

Några ekvationer i log-polära koordinater

Laplaces ekvation

Laplaces ekvation i två dimensioner kan i kartesiska koordinater skrivas

${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0}$

medan samma ekvation i polära koordinater har det mer komplicerade utseendet

${\displaystyle r{\frac {\partial }{\partial r}}\left(r{\frac {\partial u}{\partial r}}\right)+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0}$

eller ekvivalent

${\displaystyle \left(r{\frac {\partial }{\partial r}}\right)^{2}u+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0}$

Från sambandet ${\displaystyle r=e^{\rho }}$ följer dock att ${\displaystyle r{\frac {\partial }{\partial r}}={\frac {\partial }{\partial \rho }}}$ så att Laplaces ekvation i log-polära koordinater har formen

${\displaystyle {\frac {\partial ^{2}u}{\partial \rho ^{2}}}+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0}$

d.v.s. samma enkla form som i kartesiska koordinater. Detta är fallet för alla koordinatsystem där koordinattransformationen till kartesiska koordinater ges av en konform avbildning. För ett område i planet med rotationssymmetri, till exempel en cirkelskiva, är därför log-polära koordinater det naturliga valet då man betraktar Laplaces ekvation.

Cauchy-Riemanns ekvationer

En snarlik situation uppstår då man betraktar analytiska funktioner. En analytisk funktion ${\displaystyle f(x,y)=u(x,y)+iv(x,y)}$ skriven i kartesiska koordinater uppfyller Cauchy-Riemanns ekvationer:

${\displaystyle {\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}},\ \ \ \ \ \ {\frac {\partial u}{\partial y}}=-{\frac {\partial v}{\partial x}}}$

Om funktionen istället uttrycks i polär form ${\displaystyle f(re^{i\theta })=Re^{i\Phi }}$ får Cauchy-Riemanns ekvationer den mer komplicerade formen

${\displaystyle r{\frac {\partial \log R}{\partial r}}={\frac {\partial \Phi }{\partial \theta }},\ \ \ \ \ \ {\frac {\partial \log R}{\partial \theta }}=-r{\frac {\partial \Phi }{\partial r}},}$

Precis som i fallet med Laplaces ekvation, återfås den enkla formen i kartesiska koordinater genom att byta polära mot log-polära koordinater (låt ${\displaystyle P=\log R}$):

${\displaystyle {\frac {\partial P}{\partial \rho }}={\frac {\partial \Phi }{\partial \theta }},\ \ \ \ \ \ {\frac {\partial P}{\partial \theta }}=-{\frac {\partial \Phi }{\partial \rho }}}$

Cauchy-Riemanns ekvationer kan också sammanfattas i en enda ekvation som

${\displaystyle \left({\frac {\partial }{\partial x}}+i{\frac {\partial }{\partial y}}\right)f(x+iy)=0}$

Genom att uttrycka ${\displaystyle {\frac {\partial }{\partial x}}}$ och ${\displaystyle {\frac {\partial }{\partial y}}}$ i termer av ${\displaystyle {\frac {\partial }{\partial \rho }}}$ och ${\displaystyle {\frac {\partial }{\partial \theta }}}$ kan denna ekvation skrivas i den ekvivalenta formen

${\displaystyle \left({\frac {\partial }{\partial \rho }}+i{\frac {\partial }{\partial \theta }}\right)f(e^{\rho +i\theta })=0}$

Eulers ekvation

Då man vill lösa Dirichlets problem i ett område med rotationssymmetri tillämpar man vanligen separationsmetoden för partiella differentialekvationer på Laplaces ekvation i polär form. Det innebär att man skriver ${\displaystyle u(r,\theta )=R(r)\Theta (\theta )}$. Detta separerar Laplaces ekvation till två ordinära differentialekvationer

${\displaystyle {\begin{cases}\Theta ''(\theta )+\nu ^{2}\Theta (\theta )=0\\r^{2}R''(r)+rR'(r)-\nu ^{2}R(r)=0\end{cases}}}$

där ${\displaystyle \nu }$ är en konstant. Den första har konstanta koefficienter och är därför enkel att lösa. Den andra är ett specialfall av Eulers ekvation:

${\displaystyle r^{2}R''(r)+crR'(r)+dR(r)=0}$

där ${\displaystyle c,d}$ är konstanter. Denna löses vanligen med ansatsen ${\displaystyle R(r)=r^{\lambda }}$. Men genom att använda log-polär radie kan denna ekvation överföras till en ekvation med konstanta koefficienter:

${\displaystyle P''(\rho )+(c-1)P'(\rho )+dP(\rho )=0}$

I fallet med Laplaces ekvation gäller att ${\displaystyle c=1}$ och ${\displaystyle d=-\nu ^{2}}$ så att ekvationen för ${\displaystyle r}$ får den enkla formen

${\displaystyle P''(\rho )-\nu ^{2}P(\rho )=0}$

Löser man Dirichlets problem i kartesiska koordinater är det just de här två ekvationerna man får för ${\displaystyle x}$ och ${\displaystyle y}$. Återigen ser vi att den naturliga motsvarigheten till kartesiska koordinater för ett område med rotationssymmetri inte är polära utan log-polära koordinater.

Diskret geometri

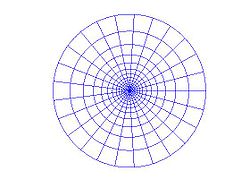
När man till exempel vill lösa en partiell differentialekvation numeriskt i ett område, behöver man införa ett diskret koordinatsystem i detta område. Om området ifråga är rotationssymmetriskt och man vill ha ett rutnät bestående av rektanglar, är polära koordinater inte särskilt användbara eftersom de inte ger någon bra indelning av en cirkelskiva i rektanglar. Anledningen till detta är att man i cirkelns centrum får trianglar snarare än rektanglar. Detta kan avhjälpas med log-polära koordinater på följande sätt. Dela in planet i ett rutnät av kvadrater med en sidlängd 2${\displaystyle \pi }$/n, där n är ett positivt heltal. Använd sedan den komplexa exponentialfunktionen för att skapa ett log-polärt rutnät i planet. Vänstra halvplanet kommer då avbildas på enhetsskivan, och antalet radier är n. Om rutnätet är parallellt med koordinataxlarna och innehåller origo, får man bilden till höger. Det kan vara än mer fördelaktigt att istället avbilda diagonalerna i kvadraterna i detta rutnät, vilket ger ett diskret koordinatsystem i enhetsskivan bestående av spiraler, se bilden nedan till höger.

Dirichlet-Neumannfunktion

Ett exempel där det sistnämnda koordinatsystemet är lämpligt är i samband med Dirichlet-Neumannfunktioner. Om det diskreta koordinatsystemet tolkas som en oriktad graf^{[särskiljning behövs]} i enhetsskivan, kan det ses som en modell för ett elektriskt nätverk. På varje båge i grafen anges en konduktans, given av en funktion ${\displaystyle \gamma }$. Det elektriska nätverket kommer då ge en diskret modell av Dirichletproblemet i enhetsskivan, där Laplaces ekvation motsvaras av Kirchhoffs lag. I noderna på cirkelskivans rand läggs en elektrisk potential (Dirichlet-data), vilket ger en elektrisk ström genom dessa randnoder (Neumann-data). Den linjära funktion ${\displaystyle \Lambda _{\gamma }}$ som avbildar Dirichlet-data på Neumann-data kallas för en Dirichlet-Neumannfunktion, och beror på nätverkets topologi samt konduktans.

I fallet med den kontinuerliga skivan, gäller att om konduktansen är likformig, säg ${\displaystyle \gamma =1}$ överallt, så uppfyller Dirichlet-Neumannfunktionen följande ekvation:

${\displaystyle \Lambda _{\gamma }^{2}+{\frac {\partial ^{2}\ }{\partial \theta ^{2}}}=0}$

För att ge en diskret modell av Dirichletproblemet som återspeglar det kontinuerliga fallet, vore det därför önskvärt att hitta en graf i enhetsskivan, vars (diskreta) Dirichlet-Neumannfunktion har samma egenskap. Medan polära koordinater inte ger något naturligt svar på denna fråga, är det just vad det spiralformade nätverket givet av log-polära koordinater förser oss med. ^[1]

Bildanalys

Redan under slutet av 1970-talet gavs tillämpningar inom bildanalys för det diskreta spiralformade koordinatsystemet givet ovan. Att representera en bild digitalt i detta koordinatsystem snarare än i kartesiska koordinater ger beräkningstekniska fördelar vid rotation och zoomning i en bild. Det kan också nämnas att fotoreceptorerna i näthinnan i det mänskliga ögat är fördelade i ett mönster med stora likheter med detta spiralformade koordinatsystem. ^[2]

Källor

• Henrik Jansson - Canonical Coordinates for Harmonic Analysis in the Continuous and Discrete Disks^{[död länk]}

Noter